In my previous post opens a new window , I mentioned how I was having issues with populating my random maze. The main problem is that there isn’t a clear way to programmatically add random rooms and paths between those rooms. I ended up with a method way more complex than I wanted and that only did the most basic thing, which was to add random types of rooms and just connect them randomly as well, but without verifying any form of room placement, for example.

This is a clear sign that we need another layer of abstraction. We need something that can hold our maze data and to take care of placing the rooms and connecting them according to the rules we establish. After some research, I think I found the right alternative: the Graph.

What are graphs?

Generally speaking, a graph consists of a set of vertices or nodes that can be interconnected by a set of edges. There are many types of graphs, but, as a data type, graphs usually implement the concepts of undirected graphs and directed graphs.

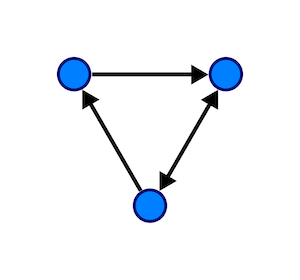
Undirected graphs are those whose edges don’t have a specific direction. As such, if nodes 1 and 2 of a graph are connected this way, it means we have a path going from 1 to 2 and that same path would allow us to go back, from 2 to 1.

In a directed graph, however, edges do have directions, and an edge that goes from 1 to 2 won’t allow you to move back, you’ll need to add a directed edge from 2 to 1.

The only other concepts concerning graphs that are of interest to us are the definitions of adjacency and a path.

Adjacency, as the name says, is the characteristic that two nodes can have which means that they are connected by an edge.

Finally, a path merely represents a sequence of edges that connect any two nodes of our graph.

Why use them?

In general, graphs are the data structure to go to when we care not so much about how data is stored but more about how it’s connected.

In our specific case, we want to generate a set of rooms that should be connected to each other. Indeed, if we wanted a really quirky experience, we could just have them all connect to other rooms without any regard for positioning and, while I do kind of like that idea, I want to be able to have a more structured approach.

Basically, my requirements are:

1. Rooms (nodes) must have a limit to the number of doors (edges) they can have (4, for starters)

2. I want them to be in a square grid. This implies that some pairs of rooms can’t have a door connecting them

3. I want to be able to “grow” the maze by starting with a single room and then randomly adding adjacent rooms until I have my maze

Also, since my doors are edges, it makes sense to me that the graph we implement is undirected, since I want the player to be able to just cross back and forth through any given door.

Now, graphs don’t implement all the rules that satisfy these requirements, but they make it way easier to encode this information. That’s what we call separation of concerns. Our little maze builder will take care of determining the rules of generating rooms, walls and doors, and the Graph class will be responsible for holding the connection information itself.

Basic operations and some design decisions

Now that we know what a graph is and why we’d want to use it, I want to briefly discuss what we need our graph to do.

Operations

Like other data structures, a graph implementation must provide us with a minimal set of operations that will allow us to use it. Since this list may vary according to one’s needs, I decided to go with this list opens a new window :

1. adjacent(x, y) - Tests whether there’s an edge between nodes x and y
2. neighbors(x) - Lists all nodes adjacent to x
3. add_node(x) - Adds node x, if it isn’t present
4. remove_node(x) - Removes node x, if it is present
5. add_edge(x, y) - Adds an edge between nodes x and y
6. remove_edge(x, y) - Removes the edge between nodes x and y
7. get_node_value(x) - Returns the value associated with node x
8. set_node_value(x, v) - Sets the value v to node x
9. get_edge_value(x, y) - Returns the value associated with the edge between x and y
10. set_edge_value(x, y, v) - Sets the value v to the edge between x and y

Design considerations

Not all graphs are equal, however. There are a few different ways to implement the functionality listed above and which one is best will depend on what it is we’ll be using this graph for.

The main decision comes to how we’ll represent this graph in memory (and in code, for that matter).

There are two common ways to do so:

1. Adjacency list: Nodes are stored as records or objects and each node holds a list of adjacent nodes. If we desire to store data on edges, each node must also hold a list of their edges and each edge will store its incident nodes.

2. Adjacency matrix: A two-dimensional matrix where the rows represent source nodes and columns represent the destination nodes. The data for nodes or edges must be stored separately.

Each approach has pros and cons to it.

The adjacency list is usually the one used for most applications, since it’s faster to add new nodes and edges and, if it’s not too big, removing nodes and edges are operations that take a time proportional to the number of nodes or edges. However, if your main use case is to add or remove edges, or lookup if two nodes are adjacent, the adjacency matrix is best. Its main drawback is that it’s the one that consumes the most memory.

The rule of thumb is: if you have a lot of edges compared to nodes (a dense graph), the adjacency matrix is preferred. If your graph is sparse (way more nodes than edges), the adjacency list is the way to go.

In our case, our graph can be either. But since mazes are usually better if we have more paths (i.e. more edges), we’ll usually have more dense graphs than not, which is why I intend to implement our graph using the adjacency matrix.

Conclusion

I’ll end this article here. I felt that the subject matter was too extensive to cover graph theory, our design decisions and our implementation. In Part 2 I’ll write about the code related to graphs.